Calkin Wilf Tree
Seminar-talks Hi, today we will discuss about Calkin-Wilf tree. I gave this talk at CMI STEMS final camp 2024.
Contents
Definitions
Before proceeding, we must be clear about what our title means.
What do you mean by Counting?
What do we mean by the term counting? We are going to prove that Rational numbers are countable. That is, there is a bijection between natural numbers and rational numbers.
Note that every bijection from set $X$ to a set $Y$ also has an inverse function from set $Y$ to set $X$.
But how are we going to create the bijection?
We will first create a bijection between the Natural numbers and Positive rationals. Let $f(1),f(2),\dots $ be the mapping from natural numbers from $\Bbb{N}\rightarrow +\Bbb{Q}$. Then, note that there is also a bijection from $\Bbb{N}\rightarrow -\Bbb{Q}$ by simply mapping $i\in \Bbb{N}\rightarrow -f(i)$.
And to create the bijection from $g:\Bbb{N} \rightarrow \Bbb{Q}$, consider
\begin{equation}
g(n)=
\begin{cases}
f(k) & \text{if } n=2k, k\in \Bbb{N}
-f(k) & \text{if } n=2k+1, k\in \Bbb{N}, k>1
0 & \text{if } n=1
\end{cases}
\end{equation}
Great! So we know how to create a bijection between $\Bbb{N}\rightarrow\Bbb{Q}$ if we are given the bijection between $\Bbb{N}\rightarrow+\Bbb{Q}$. But how can we create the bijection between $\Bbb{N}\rightarrow+\Bbb{Q}$? We use the Cute tree!
Cute tree
Every node of this binary tree is assigned a positive fraction.And the starting node is $\frac{1}{1}$. If the positive fraction is $\frac{p}{q}$, then we define it’s left child as $\frac{p}{p+q}$ and the right child as $\frac{p+q}{q}$. We call the fraction $\frac{p}{q}$ as the parent of $\frac{p}{p+q}$ and $\frac{p+q}{q}$.
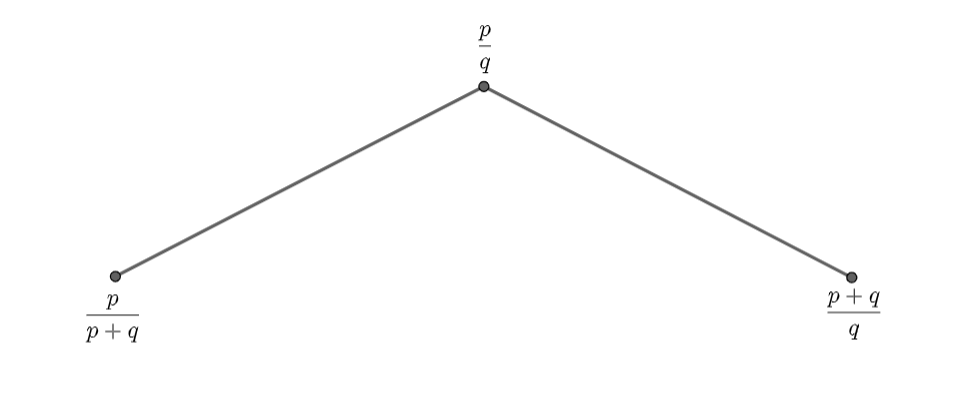
Introduction
In general, if we have the fraction as $x$, then note that it’s left child is $\frac{x}{x+1}$ and the right child is $x+1$. However, before proceeding, we shall prove this.
Infinite cute tree
We start with $\frac{1}{1}$ and proceed to make the left child and right child. Note that this process is infinite and hence the name.
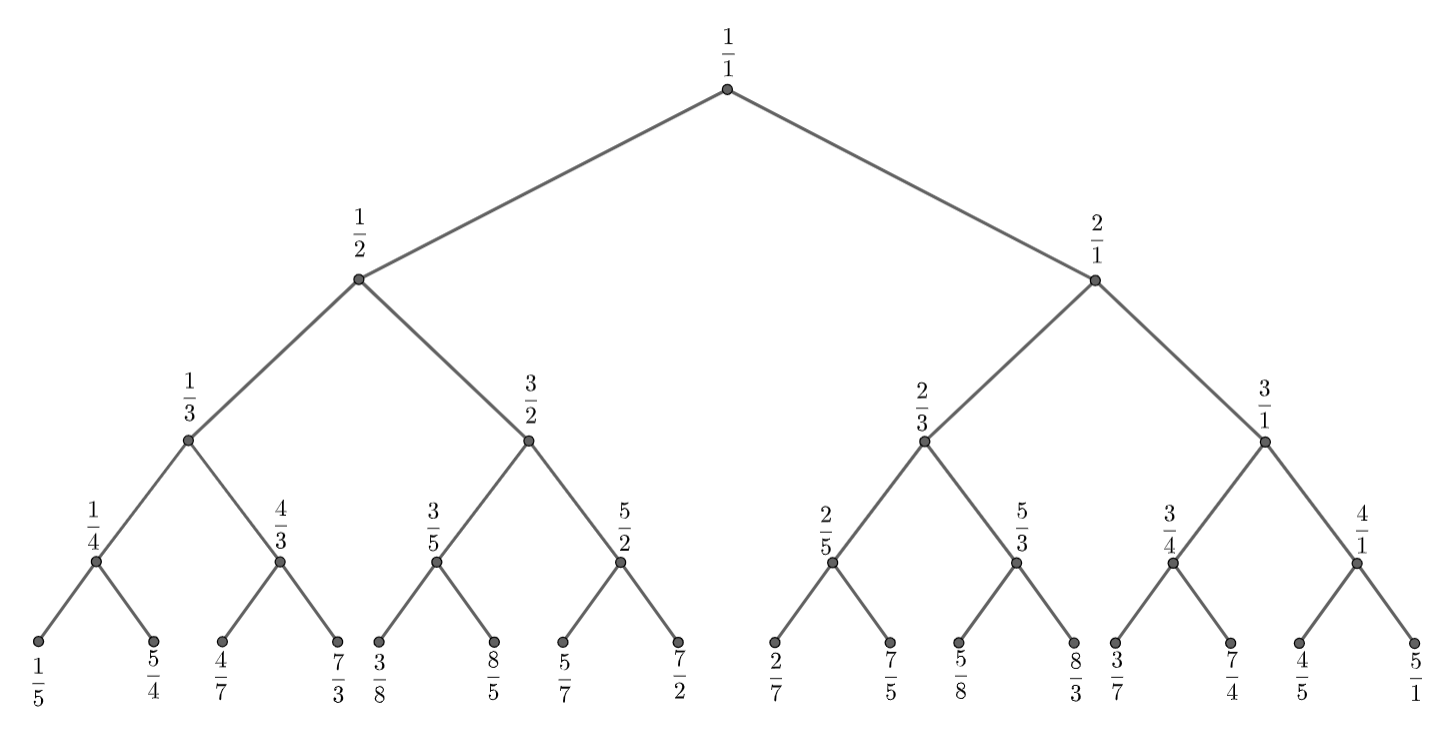
\(\vdots\)
Some properties
Here are a few properties of the infinite cute tree which we will proceed to prove in the talk.
Assuming this claim is true, we can simply number every node in every row systematically. But how are we numbering? \newline Start numbering from the first row and then number starting from the right side of the next row and continue. We get \(f(1)\rightarrow \frac{1}{1}\) \(f(2)\rightarrow \frac{1}{2}\) \(f(3)\rightarrow \frac{2}{1}\) \(f(4)\rightarrow \frac{1}{3}\) \(f(5)\rightarrow \frac{3}{2}\) \(\vdots\)
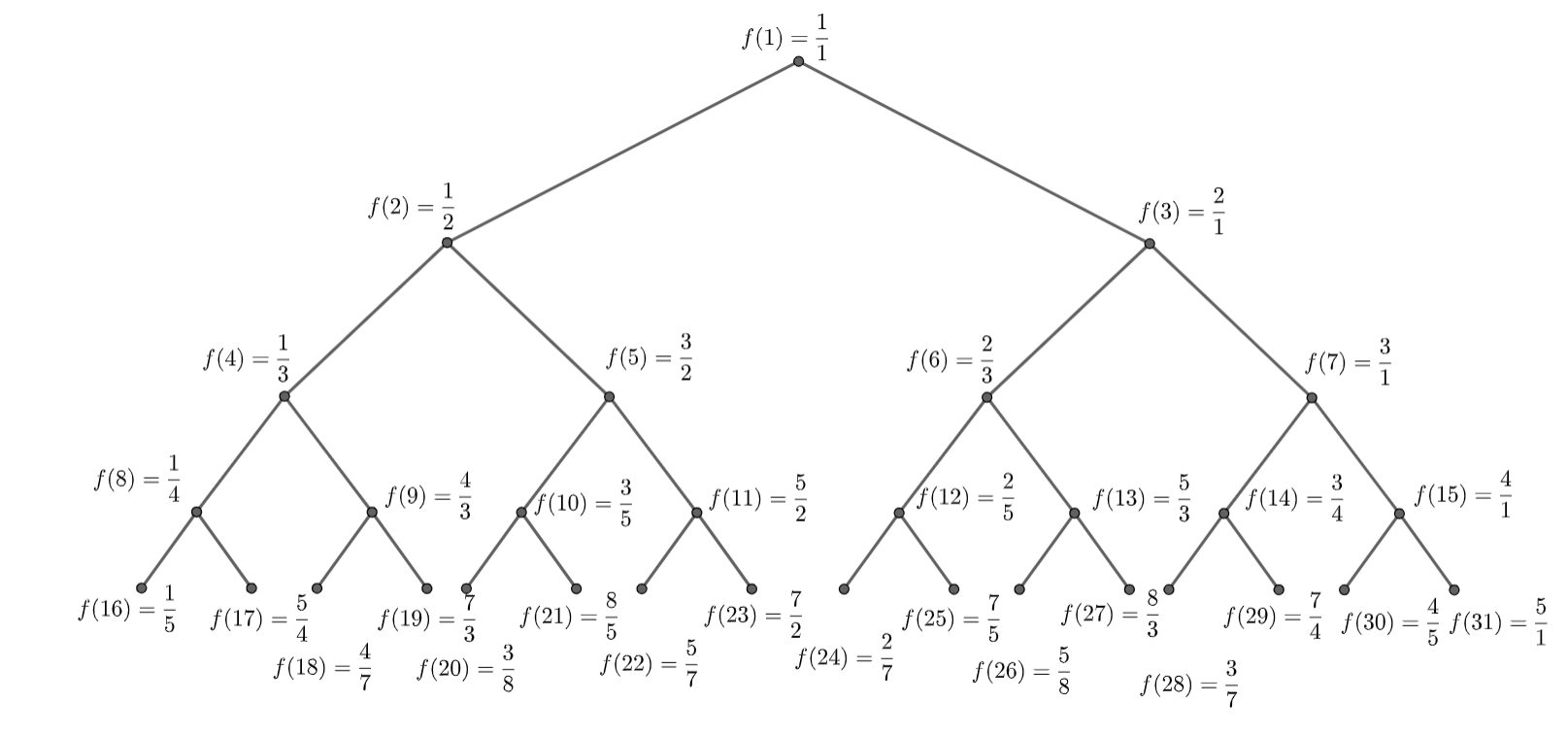
Cool sequence Algorithm
This algorithm can be used to find the unique path from any given reduced fraction to $1/1$. Moreover, this algorithm also proves the claim.
\begin{equation}
\text{For any fraction } a/b, \text{ the parent is}
\begin{cases}
a/b-a & \text{if } b>a
a-b/b & \text{if } a>b
\end{cases}
\end{equation}
For example, take any fraction, $\frac{13}{47}$ then the parent of $\frac{13}{47}$ is $\frac{13}{34}$. We will now trace it back to $1/1$ as all fractions originate from $1/1$. So we have \(13/47\rightarrow 13/34\rightarrow 13/21\rightarrow13/8 \rightarrow5/8\rightarrow5/3\rightarrow 2/3\rightarrow2/1\rightarrow1/1.\)
Note that for any fraction which appears in the tree will have a unique parent and hence a unique cool sequence path. Hence, any fraction appearing in the cute tree appears only once.
Now, we claim that any reduced fraction appears on this tree. However, note that our algorithm works for any reduced fraction.
More Properties
Binary preimage
Using our cool sequence algorithm, we showed that our function $f$ covers all positive rational numbers uniquely. Now, we will show that given any fraction, how we can find its preimage (which is obviously unique).
Remember our Cool sequence algorithm? We will do the same thing, except now we will also care about the left and right child.
For example, we know that $13/47$ is leftchild of $13/34$ and so on. So we get \(\frac{13}{47}\overset{\text{L}}{\rightarrow} \frac{13}{34}\overset{\text{L}}{\rightarrow} \frac{13}{21}\overset{\text{L}}{\rightarrow}\frac{13}{8} \overset{\text{R}}{\rightarrow}\frac{5}{8}\overset{\text{L}}{\rightarrow}\frac{5}{3}\overset{\text{R}}{\rightarrow}\frac{2}{3}\overset{\text{L}}{\rightarrow}\frac{2}{1}\overset{\text{R}}{\rightarrow}\frac{1}{1}.\) We define a new function, $g(n)$ which is basically the same as $f(n)$ but we define $g(n)$ as the following.
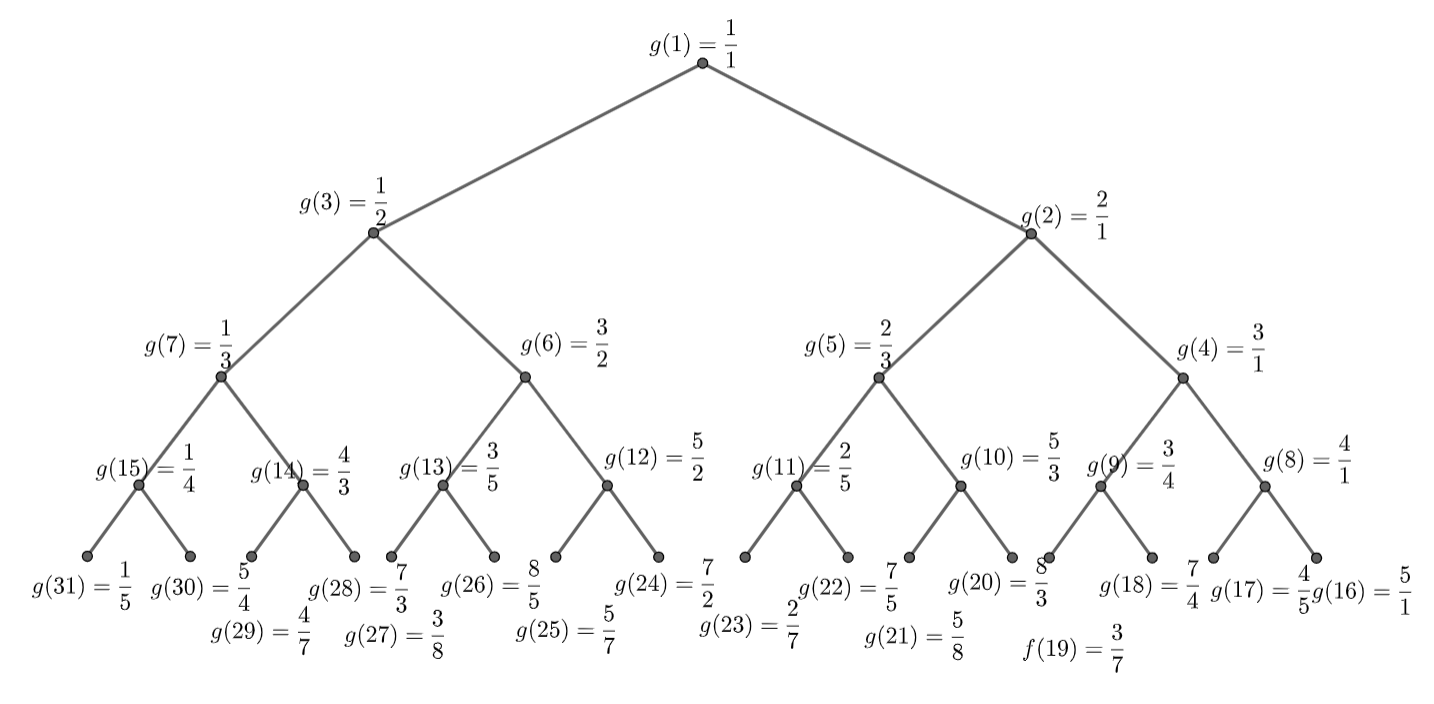
Note that \(f(n)=g(2^{\log_2(n)}+2^{\log_2(n)+1}-1-n).\) Note that if the number $g(n)$ is the parent, then its right child is $g(2n)$ and the left child is $g(2n+1)$. Now consider Now, consider the binary representation of $n,2n$ and $2n+1$. If the $n=(a_1a_2\dots a_k)_2$ then note that $2n=(a_1\dots a_k0)_2$ and $2n+1=(a_1\dots a_k1)_2$.
So we add $1$ at the end of the binary reprsentation whenever we go to the left child and $0$ if right.
Hence, for the above example, we start with $1/1$. Since $2/1$ is right child, we add $1$ to binary expression. Hence $(11)_2$. And we proceed like this.
We get that \(13/47=g((110101000)_2)=g(424)=f(512+256-1-424)=f(343).\) Note that, using our results above, we get that there is a bijection between naturals and positive rationals. And hence by our discussion, we get that there is a bijection between naturals and rational numbers. Hence, rationals are countable.
Connection with Euclidean algorithm
We consider $13/47$ as the example. Recall, we had \(\frac{13}{47}\overset{\text{L}}{\rightarrow} \frac{13}{34}\overset{\text{L}}{\rightarrow} \frac{13}{21}\overset{\text{L}}{\rightarrow}\frac{13}{8} \overset{\text{R}}{\rightarrow}\frac{5}{8}\overset{\text{L}}{\rightarrow}\frac{5}{3}\overset{\text{R}}{\rightarrow}\frac{2}{3}\overset{\text{L}}{\rightarrow}\frac{2}{1}\overset{\text{R}}{\rightarrow}\frac{1}{1}.\) Note that \(47=3\times 13+8\text{ hence three times L}\) \(13=1\times 8+5\text{ hence one time R}\) \(8=1\times5+3\text{ hence one time L}\) \(5=1\times 3+2\text{ hence one time R}\) \(3=1\times 2+1\text{ hence one time L}\) \(2=2\times 1+0\) Note that at every step, our $L,R$ are alternating. This is because if $a=qb+r$ was say $L$, then that implies the fraction was $b/a$ and then after $qL$’s we get to $b/r$, but we have $b>r$ by euclidean algorithm. So we get that $b/r$ must be a right child. Hence they are alternating.
Moreover, whenever we get the equation of the form $n=n\times 1+0$ at the end of the euclidean algorithm ( note that we are supposed to get this as the fractions are in reduced form), we write $n-1$ times the symbol. Hence, for our current example, we have $n-1=2-1=1$ times $R$.
Since we can connect euclidean algorithm and finite continued fractions, we can also connect the fractions with finite continued fractions.
Address formula
Using the binary preimage, we can now figure out the actuall address for any fraction.
For any fraction $a/b$, we figure out the $n$ such that $f(n)=a/b$. The the row $f(n)$ belongs to is ${[\log_2(n)]}+1$ as in the $k$th row, $f(2^{k-1}),\dots, f(2^{k}-1)$ are there. And then the fraction would be $n-2^{[\log_2(n)]}$th element from left.
Algebraic formula
We claim the following.
We firstly simplify the formula.
Note that for any fraction $f(n+1)$ where $f(n+1)$ is the left child, we can say that $f(n+1)=\dfrac{1}{[f(n)]+1-{f(n)}}$.
So our theorem holds true whenever $f(n)$ is a left child. Now, we see the case when $f(n)$ is the right child. Since $f(n)$ is the right child, we have $f(n+1)$ is the left child of some other parent. Since all fractions are getting generated by $1/1$, the fraction $f(n),f(n+1)$ must have same parent some rows ago. Let $a/b$ be that common parent fraction $k+1$ rows. Then note that $f(n)$ is generated by taking $k$ consecutive right childs after one left child from $a/b$ and $f(n+1)$ is generated by taking $k$ consecutive left child after one right child from $a/b$.
Now, before proceeding further, we present a lemma.
The left child of $a/b$ is $a/(a+b)$ and right child is $(a+b)/b$. As $f(n)$ is is generated by taking $k$ consecutive right childs after one left child from $a/b$, by above lemma, we have \(f(n)=a/(a+b)+k\) and we have \(f(n+1)=[(a+b)/b]/[k(a+b)/b+1]\) \(=(a + b)/(k(a + b) + b)=1/(k + b/(a+b)).\) Now, note that $[f(n)]=k$.
And hence we have \(f(n)-k=a/(a+b)\implies f(n)-[f(n)]=a/(a+b).\)
So note that \(f(n+1)=\frac{1}{1-a/(a+b)+k}=\frac{1}{1-f(n)+2k}=\frac{1}{1-f(n)+2[f(n)]}.\) Hence, we prove for the right child too.