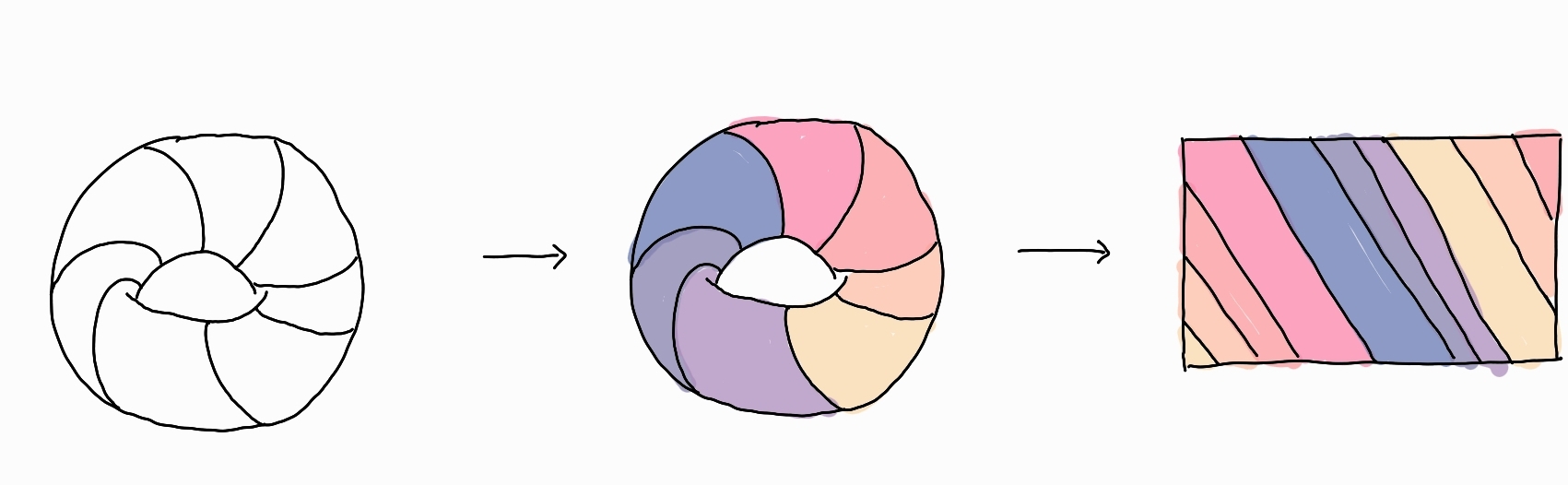
Seven Color Theorem On Torus
Graph-theory I stumbled across this while watching YouTube.
Contents
Four color theorem
We know about four color theorem, which states any planar graph is four-colorable ( vertex). Hence, by considering the dual of the graph, we get that no more than four colors are required to color map on a plane.
What about maps on torus?
There is an analogous version for maps on torus.
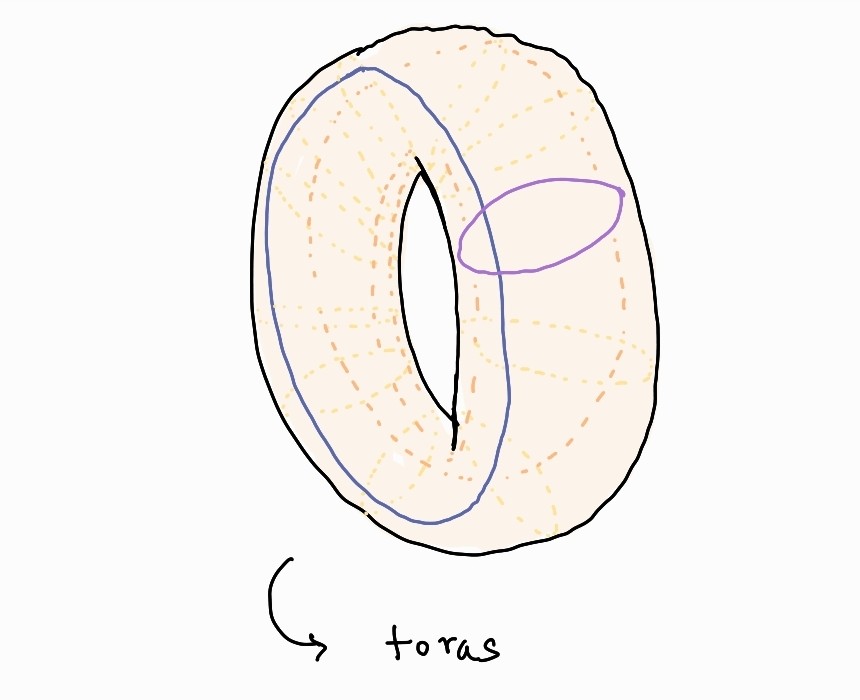
A ring torus is homeomorphic ( isomorphism, continuous inverse) to the cartesian product of two circles ( $S^1\times S^1$). It has genus $1$.
We only need 7 colors to color a graph on the torus.
A conversion is needed:
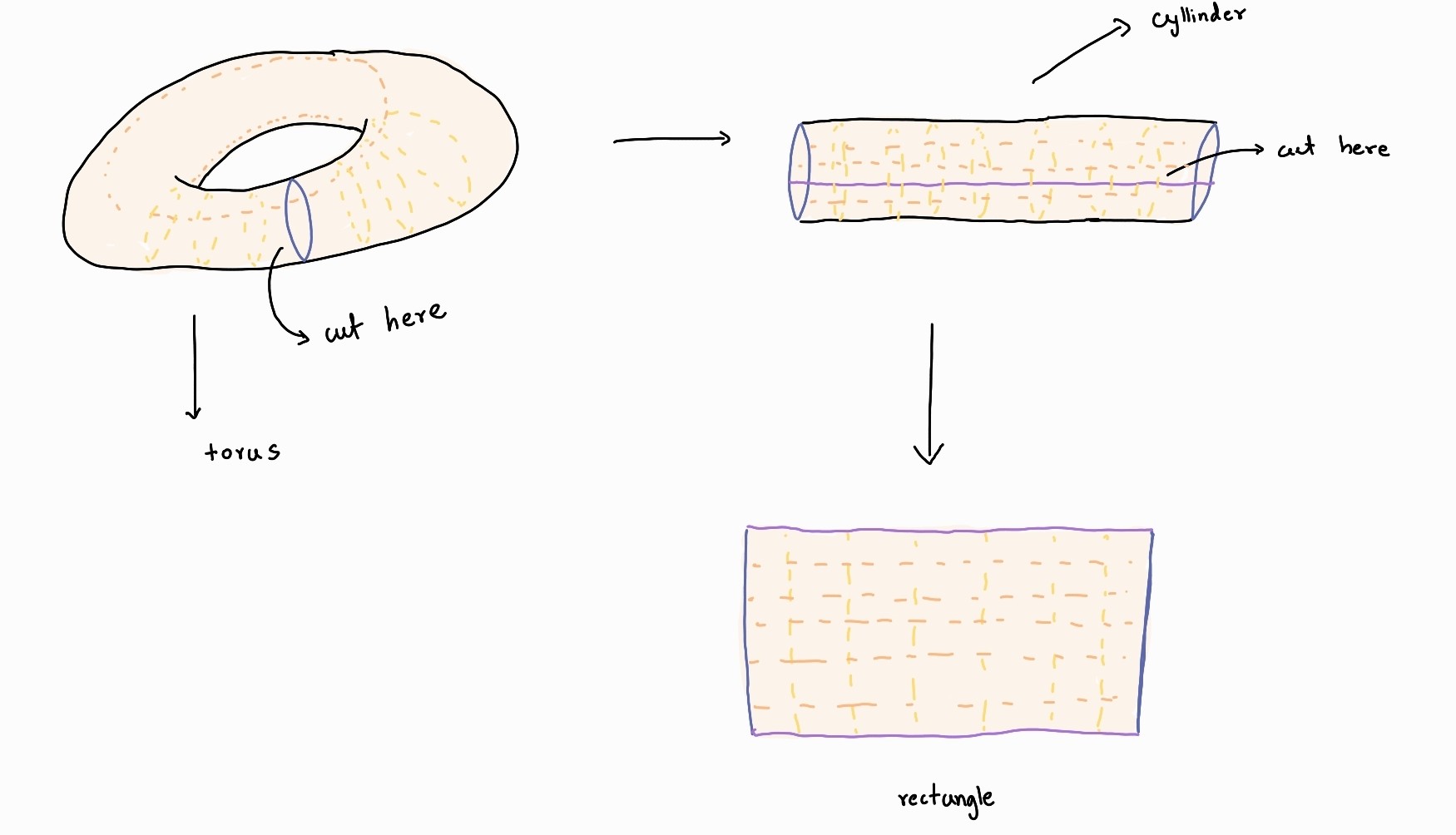
We consider the surfaces as vertices. There is an edge iff the two surfaces are neighbours ( I mean regions). Note that this graph is connected.
Note that since each edge borders atmost two faces and each face borders at least three edges $\implies 3F\le 2E$.
$$V-E+F\ge 2-2g= \chi$$ where $g$ is the number of holes in polyhedron.
Note that this is simply induction on the planar case.
Let the chromatic number of the graph be $\chi(G)=k$. Note that $\delta (G)\ge k-1$. Note that $|V|\ge k$. Note that $3F\le 2E$.
Note that $$V-E+F\ge \chi\implies V-\chi\ge E-F\implies V-\chi \ge \frac{E}{3}.$$
Note that $$\frac{E}{3}\ge \frac{(k-1)V}{6}\implies 1-\frac{\chi}{V}\ge \frac{(k-1)}{6}\implies k^2-k\le 6(k-\chi).$$
So $$0\ge k^2-7k+6\chi\implies k\le \lceil\frac{7+\sqrt{49-24\chi}}{2}\rceil.$$
About Torus
Torus has $\chi=2-2g=0$, so $k=7$. Moreover, in torus, the bound $7$ is the minimum.